The first 1000 digits of Pi:
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989
It’s that time of the year again; math teachers are freaking out, and your one weird friend is pushing up his glasses. Yup. It’s March 14th, or better known as Pi day.
Last year, I went through a phase where I was obsessed with numbers like Pi, but it was hard to find a place where I could actually go download any of it! So I read around, and eventually landed myself here, at a program called y-cruncher.
Calculating Pi
So as it turns out, from a logistical standpoint, your computer’s processor can probably crank out more digits of Pi than your internet connection can download. So it’s much more feasible to just calculate it yourself than to try to download it from anywhere. Go no further than y-cruncher, a command-line based program to calculate as much Pi as you want.
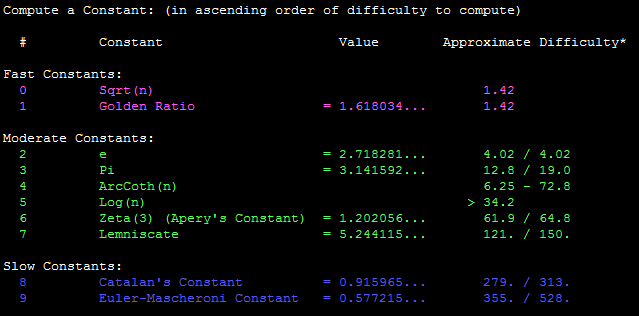
Note: y-cruncher can actually calculate a lot of constants.
If you’re on Windows, all you need to do to run y-cruncher is go to the official downloads and select the Windows version. Once it’s downloaded, you’re going to want to open up the Windows Command Prompt (just press Win+R, type in “cmd” and press Enter). Navigate to the location of the y-cruncher executable (if you’re unfamiliar with Command Prompt, use the command “dir” to show all folders/files in the current directory, and “cd [folder_name]” to navigate into a subdirectory). Once you’re there, just type “y-cruncher.exe” and it will load up the program. It will walk you through what to do, though you may need to look up more technical explanations of certain features if you’re confused. Their FAQ page is a good place to start.
If you’re running Linux, I’ll assume that you’re already pretty well versed in command-line applications. Go ahead and download the Linux variation and run that.
If you want a ridiculous amount of Pi
It should be noted that the more digits of a constant you attempt to calculate, not only will it take more time, but it will also require more system memory (RAM). Eventually, if you keep attempting to go into the higher digit counts, you’ll run out of RAM. The average person shouldn’t have this issue, but in the event that you do want to calculate a ridiculous amount of Pi (see my story about how I nearly broke my computer below), you’ll need to set up a Windows Page File or SWAP space under Linux. That is far beyond the scope of this article
That time I almost broke my computer
During my phase of “omg pi,” I quickly became obsessed with y-cruncher.
50 million digits? A cakewalk.
1 billion digits? Okay, things are getting dicey. We were getting into the range of 4 GB of RAM, which exceeded my laptop at the time. So it’s time to move the process over to my server.
5 billion digits? Eeeh. At almost 22 GB of RAM, this was testing the limits of my server, but I could handle it.
It was at this point that I decided I should step up my game. It’s no time to be fooling around. 30 billion digits, here I come. But I have a technical problem I need to solve first: not enough RAM.
A quick explanation of computer RAM
For those unfamiliar with the inner-workings of a computer, RAM (or “memory”) is an extremely fast volume of “volatile storage.” Volatile memory loses all data when power is lost. Your hard drive would be an example of “non-volatile storage,” because it retains all your data, even when you shut your computer down.
Consumer-grade computers usually only have between 4 to 8 GB of RAM, which is enough for most. Typical gaming computers can have between 16 to 64 GB of RAM, which is… excessive. Servers on the other hand, I can’t even give you a range for. They can have up to hundreds of gigabytes, even terabytes of RAM depending on what they’re used for. If you read my earlier article about my server, you’ll know that my server has 24 GB of RAM.
To calculate 30 billion digits of Pi, I’d need 138 GB of RAM, which I obviously don’t have. So what did I do? Well, I set up a thing called SWAP space. This is generally considered a safety measure for servers that aren’t supposed to crash ever. With SWAP memory enabled, when a computer runs out of RAM, it starts using the physical hard drive instead. This is much much slower and can very easily destroy your computer’s hard drive by all the reads/writes.
Okay, back to the topic
Okay, so I set up some SWAP space. I feel obligated to mention that this was an awful idea, and it almost broke my hard drive array. It’s an awfully stupid thing to read and write hundreds of gigabytes over and over, especially on a mechanical hard drive like mine. But eh, it worked out.
Thursday (5 April 2018) at 1:16 PM, I started the calculations. Aaaaand it ran.
and ran.
and ran…
Now y-cruncher does have a progress bar, which is very convenient, and it usually works… but with it using so much SWAP memory, my server was hardly functioning at all. So it basically froze after a couple of minutes, and I was left in the dark…
… for like 4 days.
But finally, on Monday (9 April 2018) at 5:02 PM, the calculations finished. There it was: a 30 GB text file that I very creatively named “pi.txt“
Y-cruncher is great, because it’s used to set records of how much of a constant people have calculated. It does so by creating a separate file called a “Benchmark Validation File,” which contains a lot of information about the computing environment and the calculation you ran. It’s very small, as it measures in the kilobytes, but contains all the information necessary to verify that you actually successfully calculated however many digits of the constant you said you did. This way, other people can quickly check to make sure that you aren’t lying without having to download several gigabytes worth of numbers and checking themselves.
This is what my validation file looks like. If you downloaded y-cruncher, you can even verify it if you want:
Benchmark Validation File - DO NOT MODIFY! If you do, it will fail validation.
Validation Version: 1.3
Program: y-cruncher v0.7.5 Build 9481
Tuning: 13-HSW ~ Airi
User: TheFuzzyFish
Operating System: Linux 4.4.0-116-generic x86_64
Processor(s):
Name: Intel(R) Xeon(R) CPU E5-2650L v3 @ 1.80GHz
Logical Cores: 1
Physical Cores: 1
Sockets: 1
NUMA Nodes: 1
Base Frequency: 1,797,908,404 Hz
Motherboard:
Manufacturer:
Model:
Version:
Serial Number: Suppressed - Personally identifiable information is opt-in only.
Memory:
Usable Memory: 1,040,441,344 ( 992 MiB)
Total Memory: Unable to Detect
Constant: Pi
Algorithm: Chudnovsky Formula
Decimal Digits: 30,000,000,000
Hexadecimal Digits: 24,914,460,712
Computation Mode: Swap Mode
Threading Mode: Push Pool -> 1 / ? (randomization on)
Working Memory: 357,702,592 ( 341 MiB)
Total Memory: 536,766,720 ( 512 MiB)
Logical Peak Disk Usage: 153,720,501,472 ( 143 GiB)
Logical Disk Bytes Read: 14,569,558,806,604 (13.3 TiB)
Logical Disk Bytes Written: 13,306,415,681,892 (12.1 TiB)
Raid-File 0/3 Settings
files : 1
buffer_per_file: 67108864
buffer_total : 67108864
Drive: 0
type : 0
files : 1
failed : 0
block : 262144
buffer_L : 256
Path : ycs-00-0
Status : 0
Start Date: Thu Apr 5 13:16:45 2018
End Date: Mon Apr 9 17:02:22 2018
Total Computation Time: 346935.017 seconds
Start-to-End Wall Time: 359136.968 seconds
CPU Utilization: 61.16 % + 2.34 % kernel overhead
Multi-core Efficiency: 61.16 % + 2.34 % kernel overhead
Last Digits:
7033207990 1471712640 1346347713 4395837248 8342882412 : 29,999,999,950
7017578801 1359424659 9118855874 7949780201 7995428606 : 30,000,000,000
Dec Counts: {3000004521,2999965727,3000003068,2999927479,2999935743,3000004401,2999991282,3000074398,3000039407,3000053974}
Hex Counts: {1557116067,1557133033,1557108796,1557162360,1557216441,1557171118,1557126615,1557142907,1557179483,1557118044,1557143787,1557129163,1557186971,1557179618,1557159558,1557186751}
Binary Hash: Floor(bin * 10^dec) mod (2^61 - 1) = 1645785335851381490
Spot Check: Good through 25,000,000,000
Timer Sanity Check: Passed
Frequency Sanity Check: Disabled in this version of y-cruncher
Reference Clock: kvm-clock
Reference Clock 0: 0
Reference Clock 1: 21,621,451
Reference Clock 2: 311,905
Is Debugger Present: Unknown
Is Contiguous: Yes
ECC Recovered Errors: 0
Event Log:
Thu Apr 5 13:16:45 2018 0.012 Reserving Working Memory
Thu Apr 5 13:16:49 2018 3.750 Reserving Working Memory: 344 MiB (locked, spread: ?)
Thu Apr 5 13:16:49 2018 3.750 Constructing Twiddle Tables
Thu Apr 5 13:16:50 2018 5.296 Constructing Twiddle Tables: 108 MiB (locked, spread: ?)
Thu Apr 5 13:16:50 2018 5.296 Allocating I/O Buffers
Thu Apr 5 13:16:51 2018 5.887 Summing Series
Thu Apr 5 13:16:51 2018 5.915 Series: ( 52 ) 0.000%
Thu Apr 5 13:16:51 2018 5.947 Series: ( 51 ) 0.000%
Thu Apr 5 13:16:51 2018 5.957 Series: ( 50 ) 0.000%
Thu Apr 5 13:16:51 2018 5.968 Series: ( 49 ) 0.000%
Thu Apr 5 13:16:51 2018 5.971 Series: ( 48 ) 0.000%
Thu Apr 5 13:16:51 2018 5.982 Series: ( 47 ) 0.000%
Thu Apr 5 13:16:51 2018 5.994 Series: ( 46 ) 0.000%
Thu Apr 5 13:16:51 2018 6.008 Series: ( 45 ) 0.000%
Thu Apr 5 13:16:51 2018 6.034 Series: ( 44 ) 0.000%
Thu Apr 5 13:16:51 2018 6.076 Series: ( 43 ) 0.000%
Thu Apr 5 13:16:51 2018 6.136 Series: ( 42 ) 0.001%
Thu Apr 5 13:16:51 2018 6.230 Series: ( 41 ) 0.001%
Thu Apr 5 13:16:52 2018 6.329 Series: ( 40 ) 0.001%
Thu Apr 5 13:16:52 2018 6.491 Series: ( 39 ) 0.001%
Thu Apr 5 13:16:52 2018 6.672 Series: ( 38 ) 0.002%
Thu Apr 5 13:16:52 2018 6.905 Series: ( 37 ) 0.002%
Thu Apr 5 13:16:52 2018 7.206 Series: ( 36 ) 0.003%
Thu Apr 5 13:16:53 2018 7.621 Series: ( 35 ) 0.004%
Thu Apr 5 13:16:53 2018 8.309 Series: ( 34 ) 0.005%
Thu Apr 5 13:16:55 2018 9.316 Series: ( 33 ) 0.007%
Thu Apr 5 13:16:56 2018 10.914 Series: ( 32 ) 0.010%
Thu Apr 5 13:16:58 2018 12.875 Series: ( 31 ) 0.013%
Thu Apr 5 13:17:01 2018 15.419 Series: ( 30 ) 0.017%
Thu Apr 5 13:17:03 2018 18.080 Series: ( 29 ) 0.022%
Thu Apr 5 13:17:07 2018 22.021 Series: ( 28 ) 0.029%
Thu Apr 5 13:17:13 2018 28.177 Series: ( 27 ) 0.038%
Thu Apr 5 13:17:23 2018 38.156 Series: ( 26 ) 0.051%
Thu Apr 5 13:17:37 2018 51.395 Series: ( 25 ) 0.067%
Thu Apr 5 13:17:55 2018 69.370 Series: ( 24 ) 0.089%
Thu Apr 5 13:18:17 2018 91.929 Series: ( 23 ) 0.118%
Thu Apr 5 13:18:54 2018 128.487 Series: ( 22 ) 0.155%
Thu Apr 5 13:19:37 2018 171.841 Series: ( 21 ) 0.205%
Thu Apr 5 13:20:36 2018 231.064 Series: ( 20 ) 0.272%
Thu Apr 5 13:22:08 2018 322.500 Series: ( 19 ) 0.359%
Thu Apr 5 13:24:11 2018 445.435 Series: ( 18 ) 0.475%
Thu Apr 5 13:27:18 2018 633.102 Series: ( 17 ) 0.628%
Thu Apr 5 13:31:28 2018 882.400 Series: ( 16 ) 0.830%
Thu Apr 5 13:37:11 2018 1225.893 Series: ( 15 ) 1.098%
Thu Apr 5 13:46:01 2018 1755.352 Series: ( 14 ) 1.452%
Thu Apr 5 13:58:09 2018 2484.059 Series: ( 13 ) 1.920%
Thu Apr 5 14:14:13 2018 3448.001 Series: ( 12 ) 2.539%
Thu Apr 5 14:37:14 2018 4828.518 Series: ( 11 ) 3.358%
Thu Apr 5 15:07:49 2018 6663.949 Series: ( 10 ) 4.441%
Thu Apr 5 15:54:07 2018 9442.291 Series: ( 9 ) 5.874%
Thu Apr 5 17:02:33 2018 13548.238 Series: ( 8 ) 7.770%
Thu Apr 5 18:42:50 2018 19564.752 Series: ( 7 ) 10.281%
Thu Apr 5 20:46:58 2018 27013.066 Series: ( 6 ) 13.606%
Thu Apr 5 23:32:22 2018 36937.183 Series: ( 5 ) 18.012%
Fri Apr 6 03:29:26 2018 51160.518 Series: ( 4 ) 23.856%
Fri Apr 6 09:16:09 2018 71964.170 Series: ( 3 ) 31.617%
Fri Apr 6 17:47:34 2018 102648.519 Series: ( 2 ) 41.944%
Sat Apr 7 05:37:37 2018 145251.335 Series: ( 1 ) 55.734%
Sat Apr 7 22:26:19 2018 205774.187 Series: ( 0 ) 74.274%
Sun Apr 8 21:26:29 2018 288583.701 Finishing Series
Sun Apr 8 21:35:17 2018 289111.820 Division
Mon Apr 9 02:05:15 2018 305309.671 InvSqrt
Mon Apr 9 04:46:42 2018 314997.091 Final Multiply
Mon Apr 9 06:50:35 2018 322430.154 Verify Final Multiply
Mon Apr 9 06:55:14 2018 322708.832 Writing hexadecimal Digits
Mon Apr 9 06:59:05 2018 322940.021 Base Converting
Mon Apr 9 13:42:58 2018 347172.759 Writing Decimal Digits
Mon Apr 9 13:48:59 2018 347534.161 Verifying Base Conversion
Mon Apr 9 16:42:26 2018 357941.214 Verifying Decimal Output
Mon Apr 9 17:02:22 2018 359136.968 End Computation
Checksum0: 53e60df1d8a6b85e6e79c09f34bae591e5bb1c49843d691c91081e516453383cb1c1afa85e9d3687bde2fbcd3955c9cfda47720e98f97a35e622be332df3aa7b
Checksum1: 798725bb0bc6e03d3f220030f7de1c5b454e739d36a62e55801058a807a05084f0cb5f165a51255673e465b03ff1ff6eecb29611ce9d98da703c72954d063af0
The recent records
Now naturally, if it was this easy for me, little highschooler Zach, to calculate 30 billion digits of Pi, other people must have calculated more, right? Well, in January of 2019, a woman by the name of Emma Haruka Iwao busted the previous record held by Peter Trueb (who had calculated 22.4 trillion digits) with a mindboggling 31.4 billion digits of Pi.
This is the most verifiable amount of Pi that has ever been calculated. If you thought my 30 GB text file was cool, Iwao made a nearly 30 TB text file. She needed a computer with 1.4 TB of RAM! Moreover, her team actually kept the digits, and made them publicly accessible! You can read all about it on their website, pi.delivery. Be glad that you have free access to the numbers that they spent over $20,000 and 4 months to calculate.
Iwao’s humor wasn’t lost on anybody. She calculated exactly 31415926535897 digits of Pi. Does that number look familiar? It’s pi^13. Marvelous.
Conclusion
Constants like Pi are really cool, and have tons of real-world applications. Regardless, we should never forget to have some fun with them. Y-cruncher is a good way to start, as it’s the exact same program used by experts to set records like Iwao.